树旋转是在中的一种子树调整操作, 每一次旋转并不影响对该二叉树进行的结果. 树旋转通常应用于需要调整树的局部平衡性的场合. 树旋转包括两个不同的方式, 分别是左旋转和右旋转. 两种旋转呈镜像, 而且互为逆操作.
平衡二叉树在进行插入操作的时候可能出现不平衡的情况,AVL树即是一种自平衡的二叉树,它通过旋转不平衡的节点来使二叉树重新保持平衡,并且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)
AVL树的旋转一共有四种情形,注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。
1. LL型
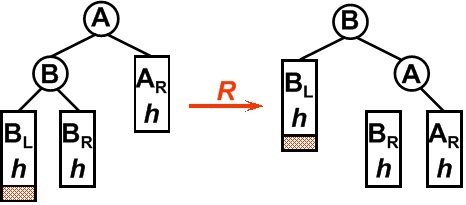
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)
2. RR型
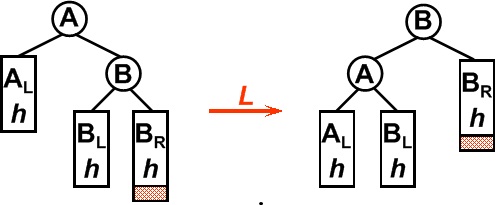
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。
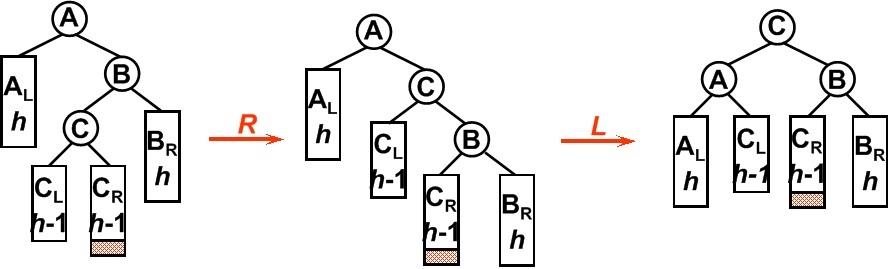
3. LR型
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
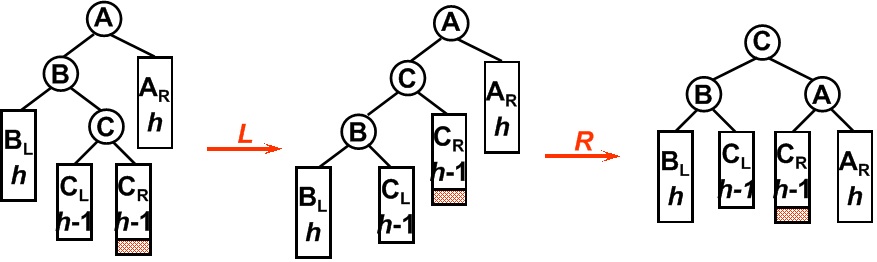
4. RL型
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。